2024医疗器械展览会Medtec解读膨体聚四氟乙烯(ePTFE)膜的微孔结构特性及其表征
2024-07-05
在1960年代开发ePTFE时,人们并不清楚为何乳化聚合的PTFE粉末在制作成膜材料时能够通过压延挤出法承受高应变率(伸长率),从而制造出多孔膜和其他形状。自那时起,针对PTFE在内的多种聚合物进行了广泛研究。这些研究结果帮助解释了PTFE对快速应变率反应的不寻常特性。
加工条件,尤其是温度和伸张速率,是决定扩张材料多孔微观结构的关键因素。2024医疗器械展览会Medtec认为这一结构包含两个基本要素:节点和细小的纤维。这些纤维将各节点相互连接。单向伸张会拉长节点,使得每个节点的长轴垂直于伸张方向(参见图1和图2)。
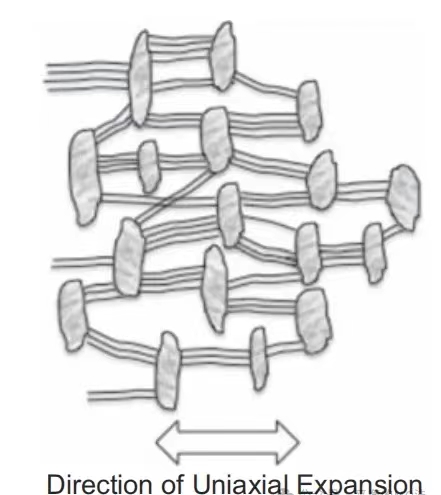
图1 单向拉伸聚四氟乙烯膜的结构示意图

图2 单向拉伸聚四氟乙烯膜的扫描电镜(1000x),箭头表示拉伸方向
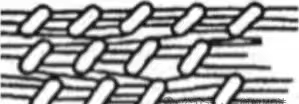
图3 双向拉伸聚四氟乙烯膜的结构示意图

图4 双向拉伸聚四氟乙烯膜的扫描电镜(1000x),垂直交叉的两条线表示拉伸方向
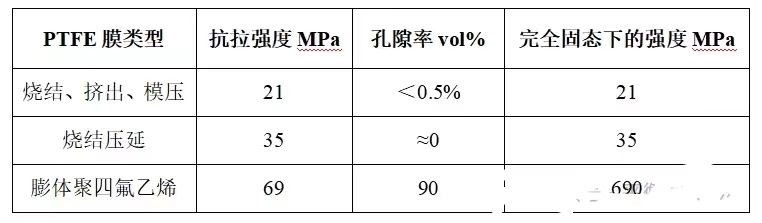
表1 不同工艺聚四氟乙烯(PTFE)膜的抗拉强度
除了极大的强度和可控制孔隙率外,ePTFE还具有很多独特特性,可以通过差示扫描量热法(DSC)进行检测。
Spruiel和Choi使用分子量为10^7的细粉PTFE进行拉伸,细粉的比重为2.149至2.165。他们向粉末中添加润滑剂,模压成型后再高压挤出,挤出物在60℃下经过压延制成PTFE板材,然后烘干去除润滑剂。
上述得到的PTFE板材在200-300℃下沿MD方向进行拉伸,部分板材只进行单轴拉伸。其他样品随后在275-325℃下,在TD方向上进行拉伸后迅速加热至略低于342℃以进行热定型,随后迅速将样品冷却至室温,并在20℃的条件下放置以促进PTFE晶体的第IV相的形成。用加热/冷却速率为10℃/min的DSC分析薄膜样品,样品重量在4至5mg的范围内。
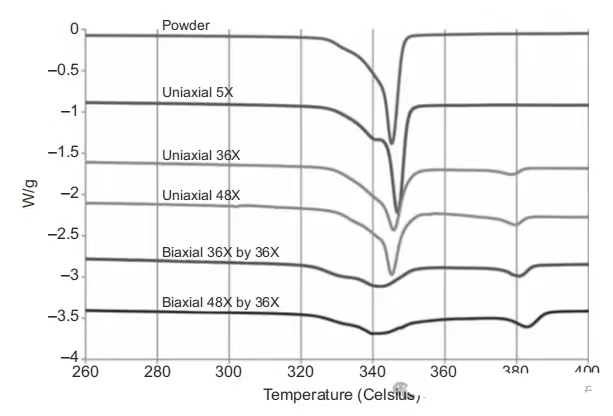
图5 DSC法分别对聚四氟乙烯粉末、单向拉伸膜和双向拉伸膜的差示扫描
(曲线上标示的数字代表拉伸比)
图5是原始板材(挤出)、单向和双向拉伸膜的DSC扫描图。
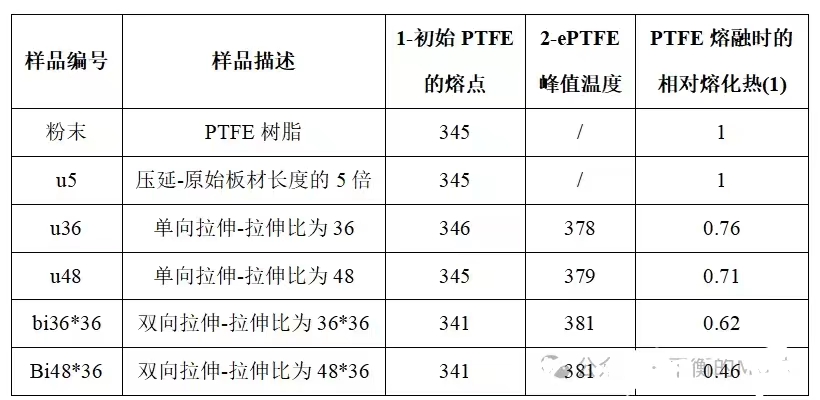
表2 PTFE粉末(1,未烧结PTFE)、ePTFE(2)的DSC法扫描得到的峰值熔点温度
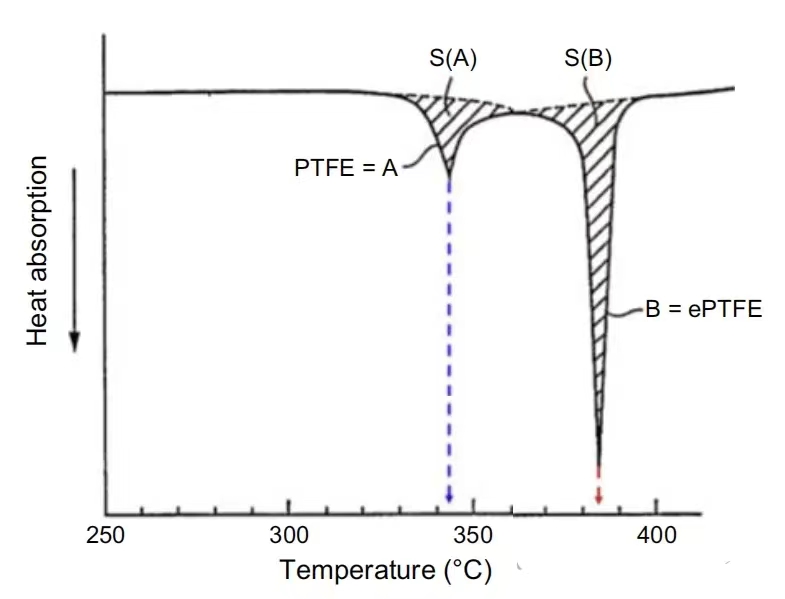
图6 DSC法热谱图显示ePTFE出现了两个温度峰,分别对应聚四氟乙烯(PTFE)(A)和膨体聚四氟乙烯(ePTFE)(B)。S(A)和S(B)代表A和B峰下曲线下的面积。
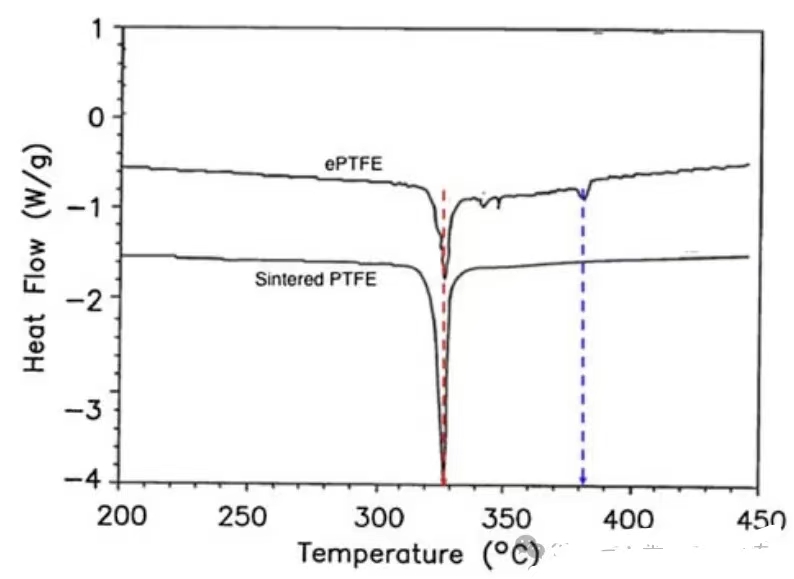
图7 PTFE粉末(烧结PTFE)与ePTFE的DSC热谱图的对比
其他研究人员提出了类似的数据,如图6和7所示。
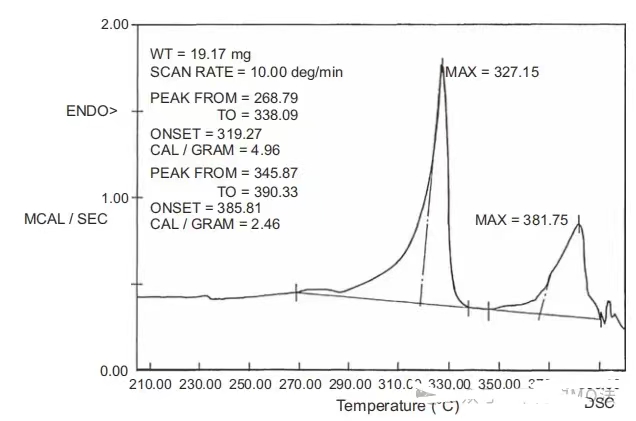
图8 完全烧结致密ePTFE DS热谱图
图8是完全烧结致密化ePTFE薄膜样品的DSC热谱图。致密化过程在拉伸之后,是将拉伸膜加压压缩后再进行烧结。在烧结过程中消除了膜样品的所有孔隙。膜的外观与标准PTFE膜类似。327.1℃和381.75℃的DSC热谱图峰值表明致密化烧结后节点和纤维的留存。这些峰值有助于验证膜样品在致密化前已经膨体化。
ePTFE的另一个独特特性是其微观结构可以通过调整树脂和工艺参数进行控制。在PTFE膜中实现所需孔径的均匀分布和平均孔径的控制,在过滤行业和其他应用中非常重要。拉伸温度和速率对孔径大小的影响尤其大,高温和高应变速率下拉伸的产品具有更均匀的结构,更小更密集的节点,节点由更多的纤维连接。
极高的抗拉强度是ePTFE产品的另一个独特属性。纤维的取向使得ePTFE的极限抗拉强度比模塑件的抗拉强度高出很多个数量级。比如,一个90%微孔PTFE膜可以轻松达到69 MPa的抗拉强度。如果考虑到孔隙率,基体强度高达惊人的690 MPa。如果只考虑ePTFE的独特特性,完全可以把它看做一种全新的材料。
早期发现,即便是最好的PTFE树脂,其结晶度也必须提高才能生产出ePTFE。适宜树脂的首要要求是具有极高的结晶度,最好是在98%或更高的范围,与之相对应的无定形含量要低。为了提升PTFE树脂的结晶度,人们开发了若干技术,如在略低于熔点的高温下进行热处理(退火)。这些方法已被证明能够在树脂膨胀加工过程中,增强其性能。
含有四氟乙烯(TFE)的共聚物,其晶体结构存在缺陷,从而导致非晶态含量增加,这些材料在制备膨体聚四氟乙烯(ePTFE)时,其性能不如纯PTFE共聚物。在膨体聚四氟乙烯(ePTFE)发展的早期阶段,并不存在专门用于最大化结晶度的特制PTFE树脂。早期ePTFE研究采用了Teflon® 6A,这是现今Teflon® 6C的前身版本,含有少于0.2%的六氟丙烯(HFP)作为共聚物。Teflon® 6A能够在接近PTFE熔点的高温下实现高速度膨胀,适合ePTFE的生产。现在,市场上已经有了专为ePTFE生产而开发的具有高结晶度的特种PTFE树脂(见表3)。
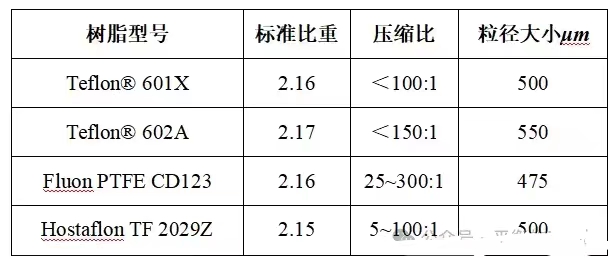
表3 用于生产ePTFE的商业聚四氟乙烯树脂示例
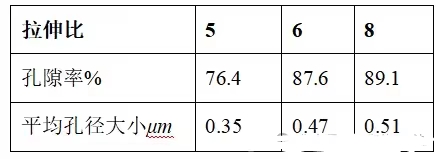
表4 机器方向上的拉伸比对孔隙率和孔径的影响
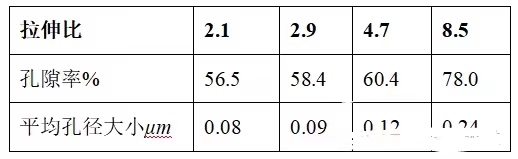
表5 横向拉伸比对孔隙率和孔隙直径的影响
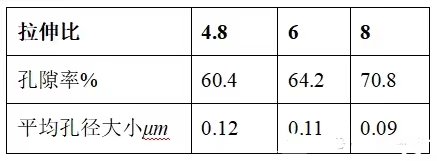
表6 横向拉伸速率对孔隙率和孔径的影响
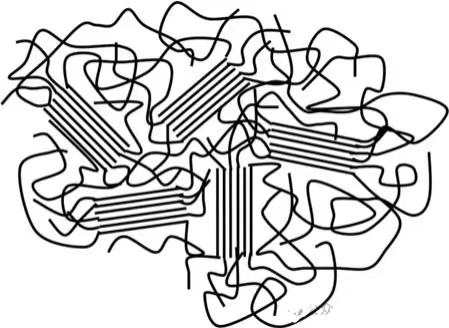
图9 半结晶热塑性高聚物的边缘微粒模型示意图
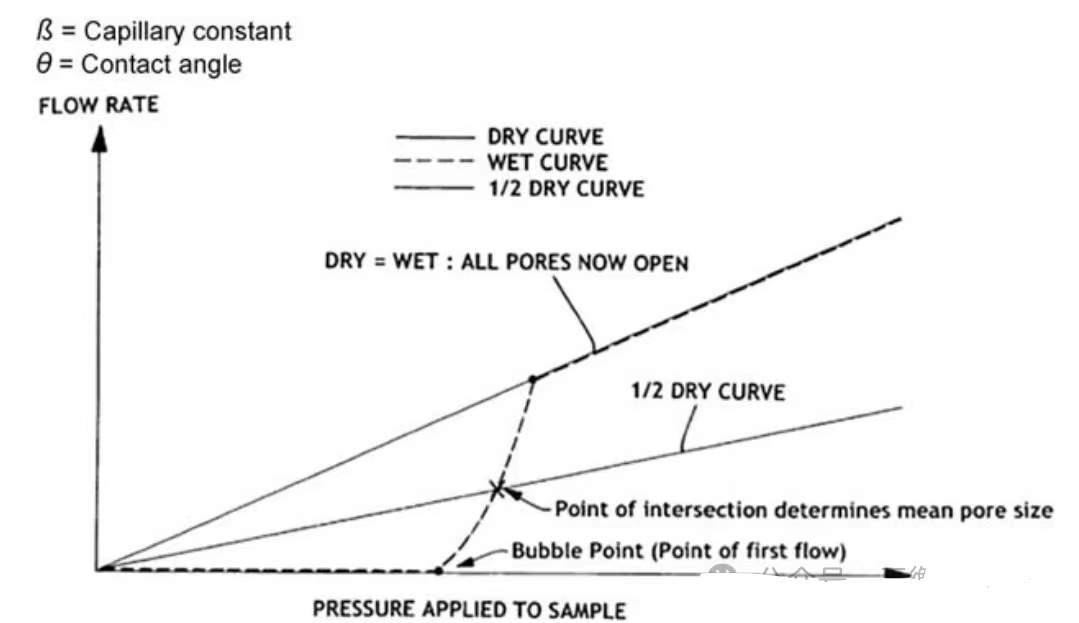
图10 典型膜的常规湿膜流量曲线、干膜流量曲线和干膜半流量曲线
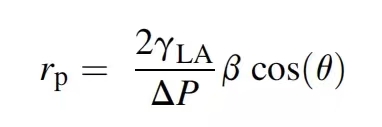 ①
①
γLA-液体表面张力(液-气),dyn/cm (mN/m)
ΔP-施加在膜两侧的压力差;β-毛细常数;θ-接触角;
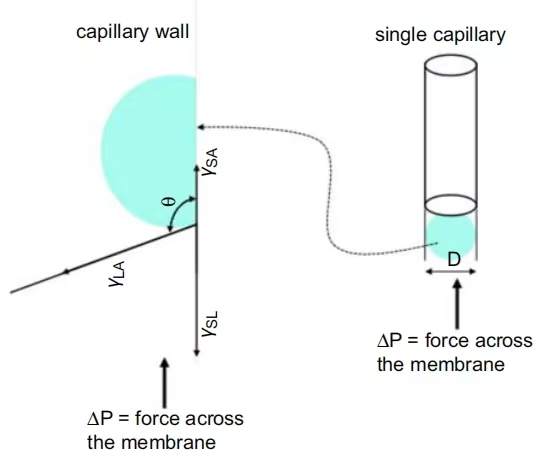
图11 液滴在圆柱形孔开口处的情况
对作用在单个孔隙毛细管壁面上的力进行平衡计算,得出的结果是:
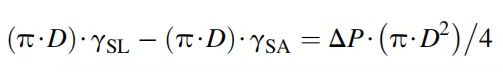 ②
②
简化后得到:
![]() ③
③
将Young-Dupre方程式:
![]() ④
④
代入方程式④并整理后,得到:
![]() ⑤
⑤
当已知 γLA、θ和ΔP的值时,可以根据方程式④计算出D。最终整理后得到:
![]()
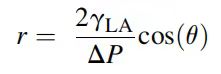 ⑥
⑥
方程式(①和⑥之间的区别在于系数 β,用于对非圆柱形孔隙形状的修正。
以下是使用方程式⑥计算水进入ePTFE微孔的最大孔径的示范。













